Sigmafunktion s

(sigma-function)

Definition 1	Die Sigmafunktion s(n) von natürlichen Zahlen entspricht der Summe aller Elemente der Teilermenge.
Beispiel 1	n=12 Þ T(n)={1, 2, 3, 4, 6, 12} Þ s(n)=1+2+3+4+6+12=28
Satz 1	p Primzahl Û s(p)=1+p
Satz 2	k habe die Primfaktorzerlegung k=paqb mit den Primzahlen p und q, a und b aus IN. Dann hat k folgende Teiler: 1 p p2 ... pa q qp qp2 ... qpa q2 q2p q2p2 ... q2pa ... ... ... ... ... qb qbp qbp2 ... qbpa In der zweiten Zeile steht das q-fache der ersten Zeile. In der dritten Zeile steht das q2-fache der ersten Zeile. Also folgt für die Summe all dieser Teiler s(k)= s(paqb)= (1+q+q2+...+qb)(1+p+p2+...+pa)= . Allgemeiner lässt sich also folgern: Habe k die Primfaktorzerlegung dann gilt für die Sigmafunktion: s(k)= Daraus folgt unmittelbar, dass s(pq)=s(p)s(q), falls p und q Primzahlen sind.
Beispiel 2	Sei k=2n, dann ist s (2n)=
Definition 2	Die verallgemeinerte Sigmafunktion s(n, k) in n.ter Potenz gibt für n=0 die Summe der Teiler einer Zahl an und sonst die Summe der Teiler in n.ter Potenz Allgemein gilt also .
Beispiel 3	s0(n) hat die Werte 1, 2, 2, 3, 2, 4, 2, 4, 3, 4, 2, 6,... für nÎ IN. s1(n) hat die Werte 1, 3, 4, 7, 6, 12, 8, 15, 13, 18,... für nÎ IN s2(n) hat die Werte 1, 5, 10, 21, 26, 50, 50, 85, 91, 130,... für nÎ IN s3(n) hat die Werte 1, 9, 28, 73, 126, 252, 344, 585, 757, 1134,... für nÎ IN
Beispiel 4	n=12. Die Teilermenge T(n)={1, 2, 3, 4, 6, 12}, also s0(n)=6 s1(n)=1+2+3+4+6+12=24 s2(n)=12+22+32+42+62+122=210
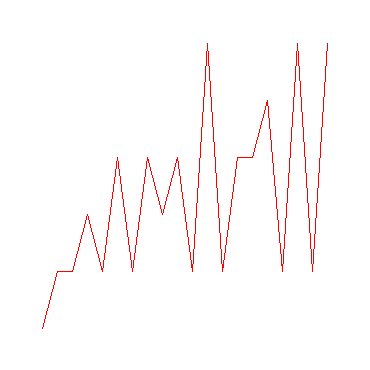
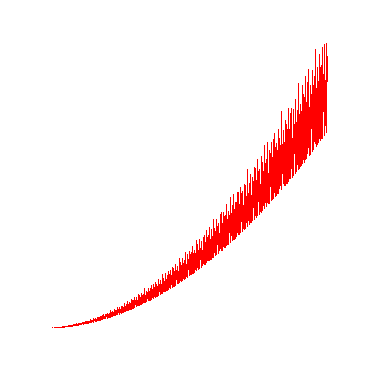
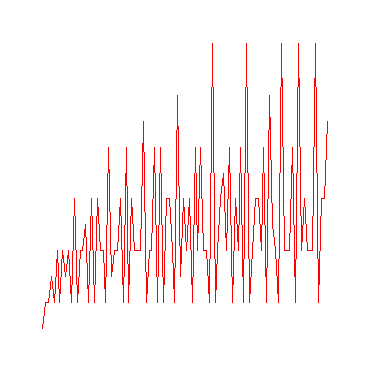
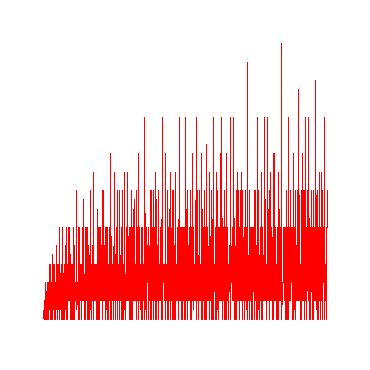
Beispiel 5	Maple-Programm zur Erzeugung der Grafik für die Anzahl der Teiler der Zahlen von 1 bis 20. k:=20: v:=array(1..k): for n from 1 to k do v[n]:=[n,sigma[0](n)]od: plot(v); Maple-Programm zur Erzeugung der Grafik für die Anzahl der Teiler der Zahlen von 1 bis 100, also k:=100: Maple-Programm zur Erzeugung der Grafik für die Anzahl der Teiler der Zahlen von 1 bis 1000, also k:=1000: Man erkennt bei all diesen Grafiken die Existenz der Primzahlen bei der Anzahl der Teiler gleich 2.
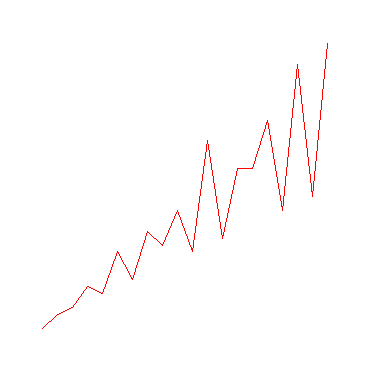
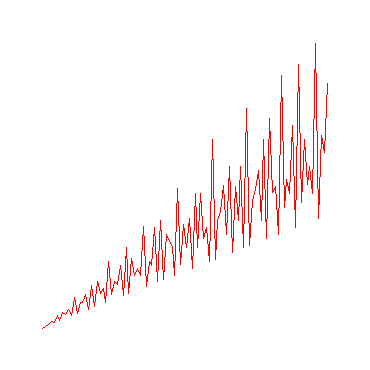
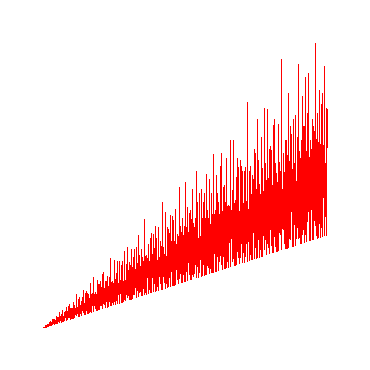
Beispiel 6	Maple-Programm zur Erzeugung der Grafik für die Summe der Teiler der Zahlen von 1 bis 20. k:=20: v:=array(1..k): for n from 1 to k do v[n]:=[n,sigma[1](n)]od: plot(v); Maple-Programm zur Erzeugung der Grafik für die Summe der Teiler der Zahlen von 1 bis 100, k:=100: Maple-Programm zur Erzeugung der Grafik für die Summe der Teiler der Zahlen von 1 bis 1000, k:=1000: Maple-Programm zur Erzeugung der Grafik für die Summe der Teiler zum Quadrat der Zahlen von 1 bis 1000, k:=1000: v:=array(1..k): for n from 1 to k do v[n]:=[n,sigma[2](n)]od: plot(v);