| Definition |
Eine Zahl kÎIN heißt Dreieckszahl, wenn sie durch ein regelmäßiges Dreieck von Punkten dargestellt werden kann. Die Dreieckszahlen sind also 1, 3, 6, 10, 15, 21, 28, 36, 45 ...
|
| Graph |
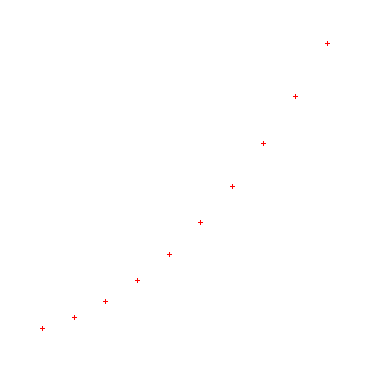
Die Dreieckszahlen haben folgende Darstellung im Koordinatensystem:
|
| Bemerkung |
Der oberen Grafik ist zu entnehmen, dass die Dreieckszahlen Tn allgemein folgendermaßen aussehen:
Also ist T3=1+2+3=6.
|
| Satz 1 |
Beweis:
also folgt  . .
|
| Satz 2 |
Beweis:
Der Binomialkoeffizient ist wie folgt definiert: 
Also ist  nach Satz 1. nach Satz 1.
|
| Beispiel 1 |
T4=1+2+3+4=10 gibt die Anzahl der Bowlingkugeln im Spiel an und das entsprechende Dreieck gibt die Anordnung an.
|
| Beispiel 2 |
T5=1+2+3+4+5=15 gibt die Anzahl der Billiardkugeln im Spiel an und das entsprechende Dreieck gibt die Anordnung an.
|
| Satz 3 |
Für die Dreieckszahlen Tn gilt folgende Rekursionsformel:
Beweis:
|
| Beispiel 3 |
|
| Satz 4 |
3Tn+Tn-1=T2n
Beweis:
|
| Beispiel 4 |
|
| Satz 5 |
3Tn+Tn+1=T2n+1
Beweis:
|
| Beispiel 5 |
|
| Satz 6 |
Beweis:
Die Quadratzahlen entsprechen aber der Summe der ungeraden Zahlen, denn es gilt
1+3+5+...+(2n-1)=s
(2n-1)+...+5+3+1=s
------------------------
n(2n-1+1)=2s
2nē=2s
nē=s
|
| Beispiel 6 |
|
| Satz 7 |
8Tn+1=(2n+1)2
Dieser Satz besagt, dass 8 gleich große Dreieckszahlen plus der Zahl 1 immer einer Quadratzahl entspricht, wie die folgenden Bilder zeigen:
  
Beweis:
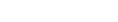
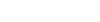
|
| Beispiel 7 |
T3=6
8T3+1=48+1=49=72=(2*3+1)2
|
| Satz 8 |
Die Summe zweier aufeinanderfolgender Dreieckszahlen ist eine Quadratzahl:
Tn+Tn-1=n2
Beweis:
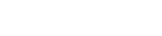
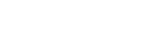
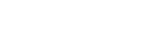
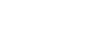
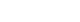
|
| Beispiel 8 |
In folgender Grafik wird dieser Satz für T3+T4 veranschaulicht.

T3+T4 =6+10=16=42
|
| Satz 9 |
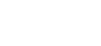
oder ohne Summenzeichen
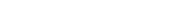
Beweis:
Vollständige Induktion
Induktionsverankerung
n=1
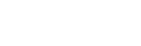
Induktionsschluss
Voraussetzung:
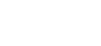
Schluss:(zu zeigen)
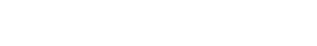
|
| Beispiel 9 |
1-3+6-10+15=9
|
| Satz 10 |
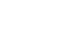
Beweis:
Da 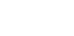 bleibt zu zeigen, dass bleibt zu zeigen, dass 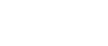
Vollständige Induktion über n
Induktionsverankerung n=1
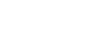 und 1=1 und 1=1
Induktionsschluss
Voraussetzung:
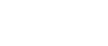
Schluss: (zu zeigen)
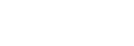
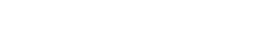
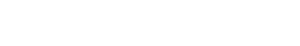
|
| Beispiel 10 |
|
| Satz 11 |
1+9Tn=T3n+1
Beweis:
|
| Beispiel 11 |
1+9T3=1+9*6=55=T10=T3*3+1
|
| Folgerung |
Da 1+9Tn=T3n+1, erzeugt folgende Formel weitere Dreieckszahlen:
9(9(9...9(9Tn+1)+1)+1)+...+1)+1
|
| Beispiel 12 |
9(9(9T3+1)+1)+1=9(9(9*6+1)+1)+1=9(9*55+1)+1=9*496+1=4456 ist eine Dreieckszahl
|
| Satz 12 |
1, 3, 21 und 55 sind die einzigen Zahlen die zugleich Dreieckszahlen und Fibonacci-Zahlen sind.
|