| Definition |
Wenn die Summe der Teiler einer natürlichen Zahl n größer 2n ist, so spricht man von einer abundanten Zahl, also:
k abundante Zahl Û s(k)>2kÛ s(k)-k>k
|
| Beispiele |
Die ersten abundanten Zahlen sind 12, 18, 230, 24, 30,..., 945,...
T12={1,2,3,4,6,12} mit Ti als Teilermenge der Zahl i,
s(12)=1+2+3+4+6+12=28>2*12 wobei s der Sigmafunktion entspricht.
|
| Satz 1 |
Alle Vielfachen einer abundanten Zahl sind wieder abundant.
|
| Folgerung |
Es gibt unendlich viele gerade abundante Zahlen, zum Beispiel alle Vielfachen von 12.
Es gibt unendlich viele ungerade abundante Zahlen, zum Beispiel alle ungeraden Vielfachen von 945.
|
| Satz 2 |
Keine Primzahl p ist eine abundante Zahl, denn s(p)=1+p<2p. Für eine abundante Zahl k gilt also s(k)>1+k und somit 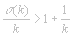 . .
|
| Satz 3 |
Jede Zahl größer als 20161 ist die Summe zweier abundanter Zahlen.
|
| Vermutung |
Es gibt vermutlich keine abundante Zahl mit der Eigenschaft s(k)=2k+1, also eine Zahl, die gerade nicht mehr vollkommen ist. Diese Zahl hieße auch leicht abundant. Das konnte aber bis heute niemand zeigen. |